Criteria for Congruence of Triangles
Criteria for Congruence of Triangles: Overview
This topic covers concepts, such as Criteria for Congruence of Triangles, SAS Criteria for Congruence of Triangles, ASA Criteria for Congruence of Triangles, Criteria for Congruence of Equilateral Triangles, etc.
Important Questions on Criteria for Congruence of Triangles
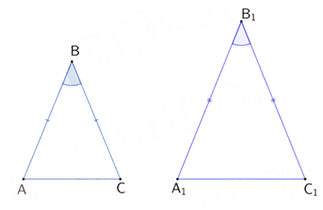
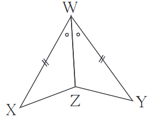
If the above two isosceles triangles are congruent and if , then find .
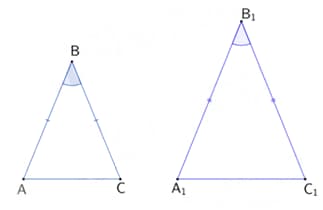
If the above two isosceles triangles are congruent and if , then find .
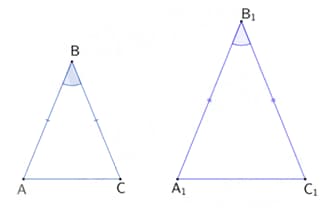
If the above two isosceles triangles are congruent and if , then find .
If the equal sides and the angle included between the equal sides of the triangles are equal to each other, then .
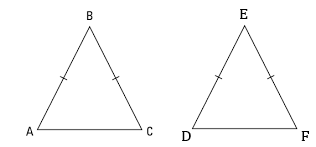
If the equal sides and the angle included between the equal sides of the triangles are equal to each other, then prove that .
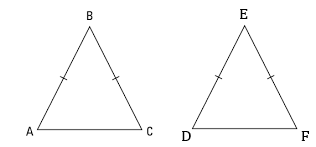
If the equal sides and the angle included between the equal sides of the triangles are equal to each other, then prove that .
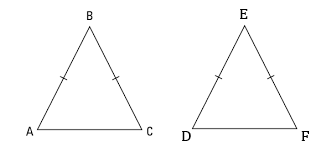
Prove that any two isosceles triangles are congruent if the equal sides and the angle included between the equal sides of the triangles are equal to each other?
If their sides are equal to each other in the two right-angled isosceles triangles given, then .
In the two right-angled isosceles triangles, prove that if their sides (other than the hypotenuse) are equal to each other?
In the two right-angled isosceles triangles, prove that if their sides (other than the hypotenuse) are equal to each other?
Prove that any two right-angled isosceles triangles are congruent if their sides are equal to each other?
What is congruence among the right-angled isosceles triangles?
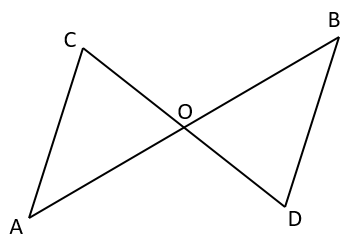
In the figure, line segments and bisect each other at . Is ?
In the given pair of triangles, parts bearing identical marks are congruent. State the test by which triangles are congruent.
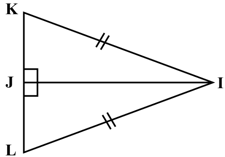
In the given pair of triangles, parts bearing identical marks are congruent. State the corresponding vertex to .
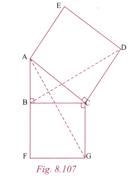
In Figure, is right angled at . and are squares. Prove that .
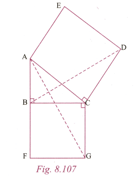
In Figure, is right angled at . and are squares. Prove that
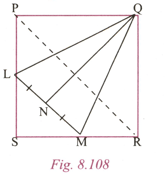
In Fig., is a square and is parallel to . is the mid point of . Prove that on producingwill pass through .
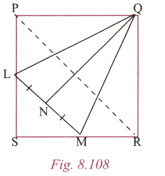
In Fig., is a square and is parallel to . is the mid point of . Prove that bisects
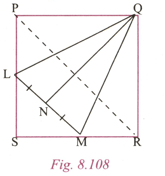
In Fig., is a square and is parallel to . is the mid point of . Prove that

